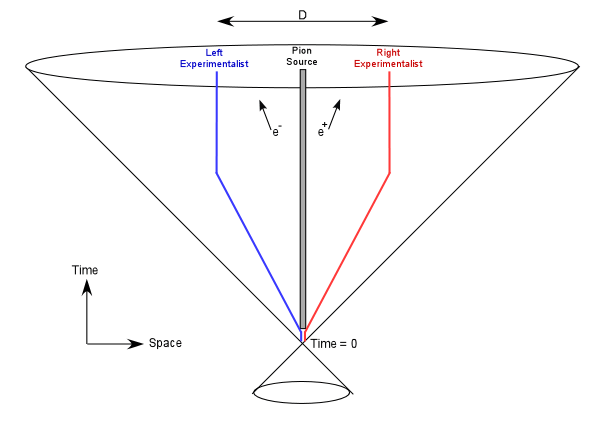
Figure 1: The Experimental Setup for an Einstein-Podolsky-Rosen Experiment
The Greatest Misconception in Science: Speeds Greater Than the Speed of Light in an Expanding Universe| Home | Books | Reports | Reviews | Contact Us | Virtual Astronomer | Press Releases |